I came across a post few days back which stated that Bayesian Methodologies are better at handling Multicollinearity in MMM.
This is simply not true.
Multicollinearity is a information redundancy problem and Bayesian methodology can’t magically solve it.
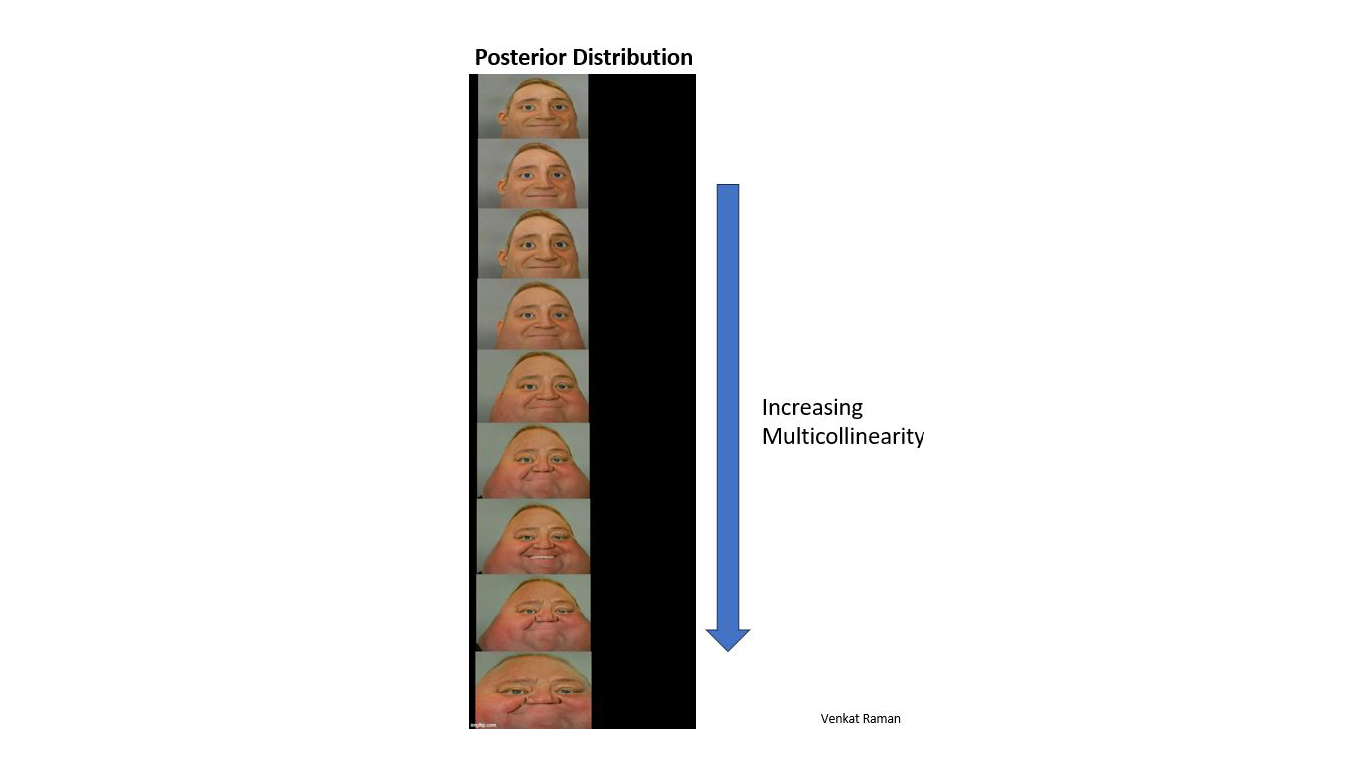
Rather the problem becomes worse in case of Bayesian MMM because your posterior distribution keeps getting wide as you have more multicollinearity.
What this means in layman terms?
Lets take an analogy:
Imagine you are on a search party to track down your pet dog that got lost in woods.
You can hear your dog barking and you set up a search radius of say 1km.
But then you also hear another dog (similar to your pet dog) barking in the woods in another direction.
Now you think of expanding your radius by another 1 km.
You see that your search of truth (or your pet dog) got much much difficult because there are same kind of barking noises (signals).
This is what happens in Bayesian MMM too. As you have multicollinearity, your posterior distribution keeps getting wide and you have no clue where the ‘true’ value lies.
Image taken from Richard McElreath’s Statistical Rethinking book.