Statisticians/Data scientists often remark “Don’t add more variables, you won’t have enough degrees of freedom”
What does that mean ?
Lets take an example of Multi linear regression
When building a multi linear regression model, adding more independent variables into the model reduces the degrees of freedom.
This is also related to the “curse of dimensionality”. Adding more variables is equal to adding more dimensions.
Your next question might be – Why is it a curse?😅
Well, the problem is, while we add more dimensions, the data we have at hand remains the same. So the data quickly becomes sparse at higher dimensions.
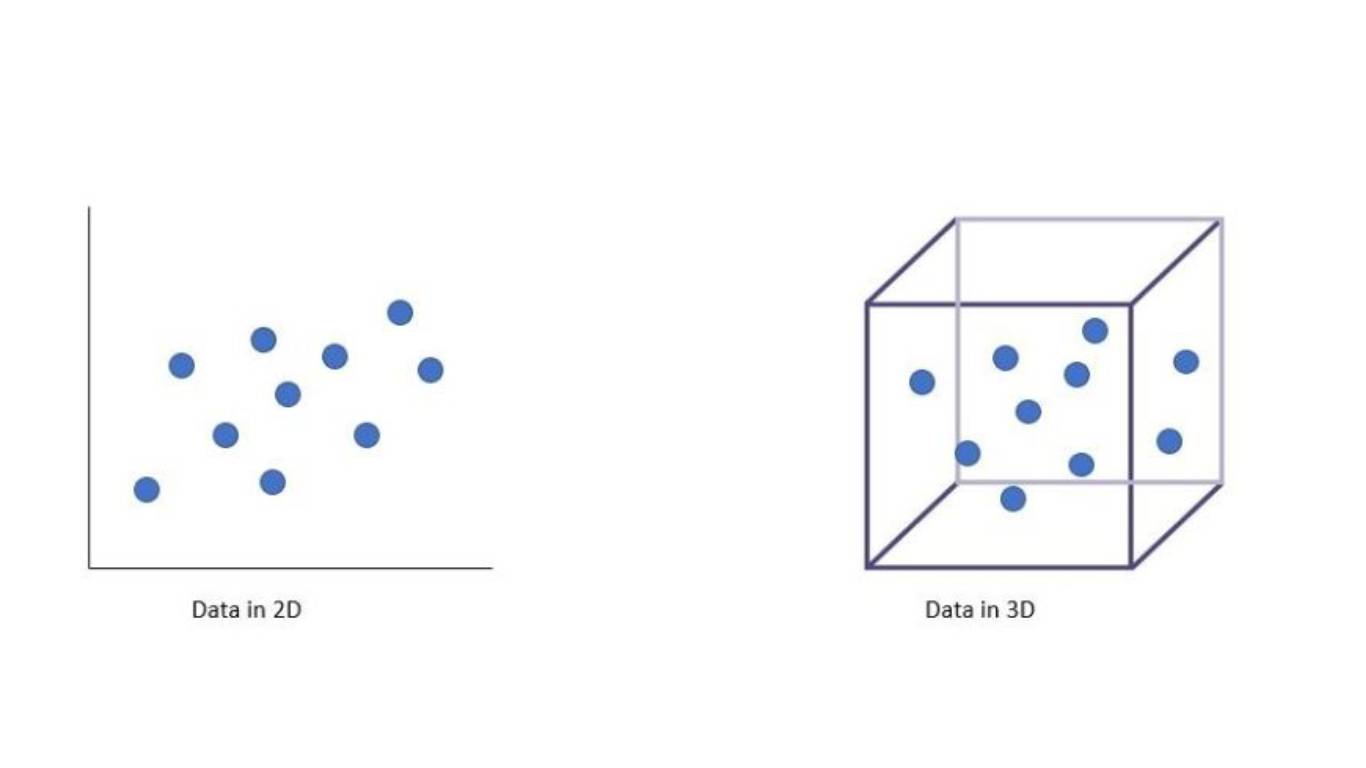
See in the image below, how the same number of data points in 2D looks dense but in 3D it starts to look very sparse.
One can imagine the sparsity in higher dimensions !!
We need more data to fill up the space, but unfortunately the data at hand is limited.
Adding more variables causes two more things:
1. Loss of degrees of freedom.
2. Highly inflated R squared value.
So now you know why statisticians are apprehensive about adding more features into the model 😅.
An intuitive explanation of Degrees of Freedom is provided in the resources section.
Resources:
Degrees of Freedom Explained: https://www.linkedin.com/posts/aryma-labs_datascience-machinelearning-statistics-activity-6823888028017266688-4xML?utm_source=share&utm_medium=member_desktop